Chemie na GJN

Vyčíslit chemickou rovnici již umíme. Víme, že musí platit zákon zachování hmotnosti a že se nám během chemické reakce atomy nemohou jen tak ztratit, mohou se pouze přeskupit do jiných částic, než jsme měli na začátku. Správně vyčíslená chemická rovnice je úplný základ a když to klapne, tak se z ní dá vyčíst velké množství informací. Vše si vysvětlíme na chemiky velmi oblíbené rovnici děje, který se nazývá pražení pyritu. Zapálili jsme kočičí zlato a vznikl nám oxid železitý a oxid siřičitý. Vyčíslená rovnice vypadá následovně:

Rovnici můžeme přečíst jako čtyři moly pyritu reagují s jedenácti moly kyslíku a vznikají dva moly oxidu železitého a osm molů oxidu siřičitého.

Na základě této rovnice dokážeme třeba říct, kolik oxidu železitého vznikne, když spálíme 20 g pyritu. Jak na to? Jak jsme si již řekli, rovnice funguje pro látková množství jednotlivých látek. Proto jako první krok většiny výpočtů spočítáme látkové množství některé ze složek. My můžeme spočítat látkové množství pyritu. Vzpomeňte/nalistujte si základní chemické výpočty.

m(FeS₂) = 20 g

M(FeS₂) = M(Fe) + 2 . M(S) = 55,85 + 2 . 32,06 = 119,97 g . mol^-1

Věřte nebo ne, ale pokud víme látkové množství jedné ze složek, umíme dopočítat všechna látková množství ostatních složek. K tomu nám pomůže stechiometrie rovnice. Dle rovnice vzniknou ze čtyř molů FeS₂dva moly Fe₂O₃, takže látková množství těchto dvou látek budou vždy vznikat v poměru 4 : 2, (což je to samé jako 2 : 1).

Kdybychom měli k dispozici:
8 molů FeS₂, vzniknou 4 moly Fe₂O₃

6 molů FeS₂, vzniknou 3 moly Fe₂O₃

1 mol FeS₂, vznikne 0,5 molu Fe₂O₃

My máme k dispozici 0,1 mol FeS₂. Látkové množství vzniklého oxidu železitého bude n(Fe₂O₃) = 0,05 mol. Hmotnost vzniklého oxidu železitého určíme pak snadno.

n(Fe₂O₃) = 0,05 mol

M(Fe₂O₃) = 2 . M(Fe) + 3 . M(0) = 2 . 55,85 + 3 . 16,00 = 143,7 g . mol^-1

A odpověď na závěr. Spálením 20 g pyritu vznikne 7,185 g oxidu železitého.

Pro jiné dvě látky můžeme použít úplně stejný princip. Třeba kyslík ku oxidu siřičitému bude vznikat v matematicky trošku nešťastném poměru 11 : 8.

Kdybychom měli k dispozici:
11 molů O₂, vznikne 8 mol SO₂

8 molů O₂, vznikne 5,82 mol SO₂

6 mol O₂, vznikne 4,36 molu SO₂

Pro jistotu uvádím i výpočet pro třetí řádek. Pokud jsou nějaká čísla v poměru 11 : 8 a vy dostanete číslo 6, které reprezentuje první hodnotu, a máte vypočítat druhou hodnotu dle daného poměru, spočítáte to jako

Zkuste si doplnit následující tabulku. Řešení naleznete na následující stránce.

Zkusme trošku svižněji jiný příklad.

Vypočtěte hmotnost uhličitanu vápenatého, kterou potřebujeme k výrobě 100 kg oxidu vápenatého, známějšího jako pálené vápno. Rovnice výroby je následující:

Krok 1) Nejprve si zkontrolujeme, že je rovnice správně vyčíslená. Ano, je.

Krok 2) Určíme látkové množství jedné ze složek. Z našeho zadání to jde pouze pro oxid vápenatý.

m(CaO) = 100 kg = 100 000 g. Nezapomeňte na správné jednotky!

M(CaO) = M(Ca) + M(0) = 40,08 + 16,00 = 56,08 g . mol^-1

Krok 3) Přes stechiometrii rovnice určíme látkové množství látky, na kterou se nás ptají. V našem případě je to uhličitan vápenatý a poměr je nejjednodušší možný a to 1 : 1. Látková množství obou látek tedy budou shodná.

Krok 4) Vypočítáme hmotnost uhličitanu vápenatého a zapíšeme odpověď.

n(CaCO₃) = 1783,17 mol

M(CaCO₃) = M(Ca) + M(C) + 3 . M(0) = 40,08 + 12 + 3 . 16,00 = 100,08 g . mol^-1

Na výrobu 100 kg páleného vápna je potřeba 178,5 kg uhličitanu vápenatého.

Řešení úkolu z předešlé stránky:

Těžší příklady jsou založené na stejném principu, jen musíte navíc použít nějakou znalost nebo vzoreček z dřívějška.

Těžší příklad by mohl vypadat třeba takto:

Jaký objem 10% kyseliny sírové (ρ_10%H2SO4= 1,066 g . cm^-3) a jaký objem 20% hydroxidu sodného (ρ_20%NaOH= 1,219 g . cm^-3) je potřeba na přípravu 15 g síranu sodného.

Krok 1) Nejprve si musíme napsat a správně vyčíslit chemickou rovnici tohoto děje. Jistě jste poznali, že se jedná o neutralizaci.

Krok 2) Ze zadání vyjádříme látkové množství některé ze složek reakce. Z našeho zadání to jde jenom pro síran sodný. Z tabulky si musíme dopočítat molární hmotnost této soli. M(Na₂SO₄) = 142 g . mol^-1.

Krok 3) Na základě stechiometrie rovnice dopočítáme látková množství látek, které potřebujeme. Před kyselinou sírovou a síranem sodným jsou jedničky (které se do rovnice nepíší). Tyto dvě látky jsou v poměru 1 : 1, a proto budou jejich látková množství totožná.

U hydroxidu sodného nalezneme v rovnici dvojku. Na jeden síran sodný tedy spotřebujeme dva hydroxidy sodné. Poměr těchto dvou látek hydroxidu a síranu je proto 2 : 1, a proto bude látkové množství hydroxidu dvojnásobkem látkového množství síranu.

Krok 4) Látková množství jednotlivých složek reakce už známe. Teď nám situaci bude komplikovat fakt, že nepracujeme s čistými látkami, ale s roztoky. Kolik bude potřeba 10% roztoku kyseliny sírové?

Nejprve si spočítáme hmotnost čisté (100%) kyseliny sírové.

Ještě jednou. Nyní jsme spočítali, kolik bychom potřebovali čisté, tzn. 100%, kyseliny. My ale používáme její 10% roztok. 10 % hmotnosti tohoto roztoku tvoří čistá kyselina, tedy našich 10,40 g a zbylých 90 % bude voda. Celý 10% roztok bude vážit

Matematicky jsme řešili problém, kolik váží celek, když 10 % váží 10,4 g.

Na objem to již s pomocí hustoty ze zadání přepočítáme snadno.

To samé provedeme s hydroxidem. Zase budeme potřebovat molární hmotnost hydroxidu sodného z tabulky. M(NaOH) = 40 g . mol^-1.

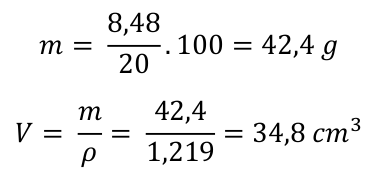
Krok 5) Odpověď. Na přípravu 15 g síranu sodného je třeba použít 97,6 ml 10% roztoku kyseliny sírové a 34,8 ml roztoku hydroxidu sodného.

Další těžší:

Jaký objem kyslíku uvolní při tepelném rozkladu 100 g dusičnanu draselného, pokud dusičnan obsahuje 5 % nečistot. Za podmínek reakce 1 mol plynu zaujme 24 dm³.

Krok 1) Správně vyčíslená rovnice děje.

Této vlastnosti dusičnanu si všimli již dávno Číňané, a proto jsou dusičnan draselný společně se sírou a uhlíkem základními složkami černého střelného prachu.

Krok 2) Spočítáme látkové množství dusičnanu, ale v zadání máme, že obsahuje 5 % nečistot. Nejprve se tedy těch nečistot matematicky zbavíme a zbude nám pouze čistý dusičnan. M(KNO₃) = 101,1 g . mol^-1.

Krok 3) Ze stechiometrie rovnice určíme látkové množství kyslíku. Poměr dusičnanu a kyslíku dle rovnice je 2 : 1. Na jednu molekulu kyslíku spotřebujeme dva dusičnany. Látkové množství kyslíku bude tedy poloviční oproti látkovému množství dusičnanu.

Krok 4) Určíme objem vzniklého kyslíku. Pokud jeden mol plynu za podmínek reakce zaujme 24 dm³, objem vzniklého kyslíku spočítáme snadno.

V(O₂) = n(O₂) . 24 = 11,28 dm³

Krok 5) Odpověď. Z uvedeného množství dusičnanu draselného se uvolní 11,28 litrů kyslíku.

Extrémní příklad:

Soda (uhličitan sodný), která se používá například při výrobě papíru, se vyrábí Solvayovým procesem. Jedná se o sled tří po sobě jdoucích dějů, které vyjadřují následující rovnice.

1. NaCl + H₂O + NH₃+ CO₂ → NaHCO₃+ NH₄Cl
2. 2 NaHCO₃→ Na₂CO₃+ H₂O + CO₂
3. NH₄Cl + Ca(OH)₂→ CaCl₂+ 2 H₂O + 2 NH₃

Kolik kg chloridu sodného je třeba na výrobu 20 kg sody (uhličitanu sodného)?

Problém, který řešíme je, že musíme pracovat s více rovnicemi. Tak pojďme na to.

Krok 1) Zkontrolujeme, zda máme všechny rovnice správně vyčíslené. Vypadá to, že ano. Pracovat budeme pouze s prvními dvěma. Třetí rovnice je pro naše řešení nadbytečná a je zde uvedena jenom proto, aby byl Solvayův proces kompletní. Tímto dějem se obnovuje/recykluje amoniak pro první proces.

Krok 2) Musíme najít pojítko mezi NaCl a Na₂CO₃. Vypadá to na sodík (přesněji sodné kationy), protože veškerý sodík z NaCl přejde v prvním ději nejprve na NaHCO₃a poté v rámci druhého děje přejde z NaHCO₃na Na₂CO₃. Musí být tedy vztah mezi látkovými množstvími NaCl, NaHCO₃a Na₂CO₃.

Zkusme to nastřelit. Zkusme si třeba představit, že máme 10 mol NaCl. Podle první rovnice budou látková množství NaCl a NaHCO₃shodná, poměr těchto látek je 1 : 1. Z 10 mol NaCl vznikne 10 mol NaHCO₃. Přecházíme na druhý děj. Poměr mezi NaHCO₃a Na₂CO₃je dle druhé rovnice 2 : 1. Z našich 10 mol NaHCO₃vznikne 5 mol Na₂CO₃. Poměry látkových množství NaCl : NaHCO₃: Na₂CO₃jsou 10 : 10 : 5 a po pokrácení 2 : 2 : 1. V klidu si to přečtěte a promyslete ještě jednou, dvakrát...

Krok 3) Máme připravit 20 kg sody. Rovnice se zapisují pro látková množství, a tak musíme hmotnost převést na látkové množství. Molární hmotnost uhličitanu sodného si zjistíme z tabulek.

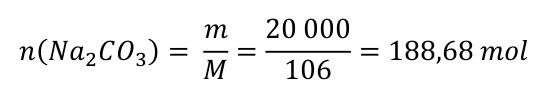
Krok 4) Dle poměru určíme látkové množství pro chlorid sodný. Poté spočítáme hmotnost chloridu sodného. Molární hmotnost chloridu sodného si zjistíme z tabulek.

Krok 5) Odpověď. Pro výrobu 20 kg sody je třeba 22,06 kg chloridu sodného.

Příklady k procvičení:

1. Kolik kilogramů surového železa se vyrobí z 10 tun oxidu železitého. Předpokládejte, že redukčním činidlem je čistý uhlík. Nevyčíslená rovnice tohoto děje je
Fe₂O₃+ C → Fe + CO₂

(6,99 tun železa)

2. Kolik kilogramů hašeného vápna lze získat z tuny vápence? Kolik by to bylo, pokud by vápenec byl o čistotě pouze 82%? Rovnice dějů jsou
Pálení vápna: CaCO₃+ → CaO + CO₂
Hašení vápna: CaO+ H₂O → Ca(OH)₂

(740 kg hašeného vápna, pokud bude vápenec znečištěný pak 606,8 kg)

3. Kolik gramů hydroxidu hlinitého vznikne vysrážením 10 g Al₂(SO₄)₃roztokem hydroxidu sodného? Nevyčíslená rovnice tohoto děje je
Al₂(SO₄)₃+ NaOH → Al(OH)₃+ Na₂SO₄

(4,56 g hydroxidu hlinitého)

4. Kolik ml 5% kyseliny dusičné o hustotě ρ = 1,03 g . cm^–3je třeba na neutralizaci 10 g hydroxidu sodného?

(305,8 ml)

5. Kolik litrů 30 % roztoku hydroxidu sodného (ρ = 1,33 g . cm^–3) bude potřeba k neutralizaci 20 litrů 62% kyseliny sírové (ρ = 1,52 g . cm^–3)?

(38,56 litrů)

6. Jaký objem acetylenu (C₂H₂) vznikne při reakci 50 g karbidu vápníku (CaC₂) s vodou? Předpokládejte, že za daných podmínek zaujme 1 mol acetylenu 22,41 dm³. Rovnice tohoto děje je
   CaC₂+ 2 H₂O → C₂H₂+ Ca(OH)₂
   (17,48 litrů)
7. Kolik litrů oxidu uhličitého vznikne rozkladem 500 g vápence s 3% obsahem nečistot? Rovnice děje je uvedena u příkladu 2. Předpokládejte, že 1 mol plynu zaujme 22,41 dm³.

(108,7 litrů)

8. Kolik m³kyslíku se spotřebuje při spálení 2 kg propanu C₃H₈? Předpokládejte, že 1 mol plynu zaujme 22,41 dm³. Nevyčíslená rovnice tohoto děje je
C₃H₈+ O₂→ CO₂+ H₂O
(5 m³kyslíku)
9. Jaký objem amoniaku NH₃získáme zahřáním chloridu amonného NH₄Cl s 5 g oxidu vápenatého CaO, je-li výtěžek reakce 90 %? Předpokládejte, že 1 mol plynu zaujme 22,41 dm³. Nevyčíslená rovnice tohoto děje je
CaO + NH₄Cl → CaCl₂+ H₂O + NH₃
(3,6 litru amoniaku)