Chemie na GJN

Asi vás nepřekvapí, že abychom mohli pracovat se směsmi, dříve či později budeme potřebovat nějaký způsob, jak přesně vyjádřit složení dané směsi. Jeden způsob používají zedníci – hoď do míchačky dvě lopaty písku a jednu cementu – jiný, trochu jemnější, způsob používají některé kuchařky – dva hrníčky mouky a jednu lžíci cukru. Taková přesnost ale chemikům nestačí, potřebujeme takovou veličinu, kterou dokážeme velmi přesně změřit (uznejte, jak byste nabrali 0,872 lopaty). Nejčastěji využívanou veličinou je hmotnost a na ní založené vyjádření složení směsi se nazývá hmotnostní zlomek .

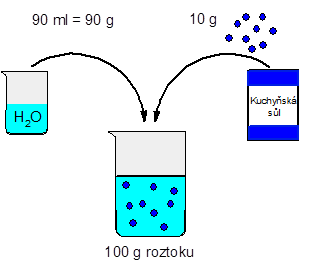
Jak to funguje? Vezměme si 10 g kuchyňské soli a rozpusťme ji v 90 ml vody (tedy 90 g vody, protože hustota vody se běžně udává jako ρ = 1 g . cm^-3). Tímto postupem získáme 100 g roztoku, protože hmotnosti složek se sčítají. Rozpuštěná látka, tedy kuchyňská sůl, tvoří 10 % hmotnosti roztoku, protože sůl váží 10 g a roztok 100 g. Máme tedy 10% roztok kuchyňské soli.

Nyní celý postup zobecníme a dáme do jednoduchého vzorečku, což se nám bude hodit, až budeme mít větší počet rozpuštěných látek nebo „méně šikovné“ hodnoty hmotností. Platí

Řešení našeho příkladu by vypadalo:

m(NaCl) = 10 g

m(H₂O) = 90 g

m_roztok= m(NaCl) + m(H₂O) = 10 + 90 = 100 g

w(NaCl) = ?

Připravili jsme 10% vodný roztok kuchyňské soli.

Všimněte si, že hmotnostní zlomek nemá jednotku. Je to bezrozměrná veličina. Důvodem je, že se jednotka hmotnosti v čitateli, pokrátí s jednotkou hmotnosti ve jmenovateli zlomku. Aby toto fungovalo, musíte všechny hmotnosti uvádět ve stejných jednotkách. Hmotnostnímu zlomku se také běžně říká hmotnostní koncentrace.

Jedná se o vaše první chemické výpočty, proto je nepodceňte. Jakmile něčemu nerozumíte, hned se ptejte. Dále se vám velmi bude hodit, když si osvojíte „rozumný“ styl zápisu příkladu. Jasně si napište, co víte ze zadání. Napište si vzorec, ze kterého vycházíte. Pište si mezivýpočty a jasně označte výsledek. Proč? Dva důvody. První je pro vás, když se spletete, tak v pečlivě vedeném postupu snadno objevenou chybu opravíte a rychle se můžete dopočítat ke správnému výsledku. Druhý je pro nás, pro učitele. Test má být jasný a výstižný, nikoliv napínavý. Pokud nám odevzdáte směsku čísel, kde některá z nich nápadně připomínají staroegyptské znaky, opravdu vám nemůžeme udělit hezkou známku.

Otázka k zamyšlení 11: Jaká může být maximální hodnota hmotnostního zlomku?

Matematické okénko, aneb co vás může potrápit:

- Jak si můžu vyjádřit to, co potřebuju ze vzorečku?Už jsme se naučili, že pro hmotnostní zlomek nějaké látky platí následující vztah

Může se ale stát, že jak hmotnostní zlomek w_A, tak hmotnost roztoku m_roztokbudeme znát, a budeme počítat hmotnost látky A, tedy m_A. To se stane třeba v případě, když máme připravit 200 g roztoku (m_roztok) o hmotností koncentraci 15 % (w_A). Kolik mám tedy látky A navážit a rozpustit?

Když se chci zbavit zlomku, vynásobím ho jeho jmenovatelem. Protože musí být zachována rovnost, musím vynásobit obě strany vztahu (když se má něco rovnat, nemůžu vynásobit jen jednu stranu vztahu a druhou nechat netknutou).

Na levé straně se mi m_roztokpokrátí a zbyde jen čitatel m_A.

Vřele doporučuji si tyto úpravy vztahů zautomatizovat, bude se vám to ještě mnohokrát hodit.

- Co mám dělat, když mám neznámou jak v čitateli, tak jmenovateli zlomku?

Nepříjemnost nastane, když máme neznámou jak v čitateli, tak ve jmenovateli. Toto se stane třeba v případě, že známe hmotnost použité vody (m_voda) a koncentraci roztoku (w_A), a nějaký šťoural se nás zeptá, kolik látky jsme tam vlastně rozpustili. Matematicky to vypadá takto

A my m_Aneznáme a co hůř je jak v čitateli, tak ve jmenovateli zlomku. Nejprve použijeme stejný trik jako v předešlém případě a zbavíme se zlomku – vynásobíme obě dvě strany vztahu jmenovatelem zlomku.

Na pravé straně se nám jmenovatel pokrátí a jsme bez zlomků. Lepší, ale ještě nemáme vyhráno.

Roznásobíme závorku. Tedy w_Avynásobíme každý člen v závorce.

Teď to trochu učešeme a můžeme to dát do kalkulačky. Snažíme se vztah upravit tak, aby to, co neznáme, bylo na jedné straně a vše ostatní na druhé. Nejprve m_Ak sobě.

Vytkneme m_A

Poslední krok, vydělíme obě strany (1 - w_A) a už můžeme dosadit číselné hodnoty, protože vše co známe, máme na jedné straně a naši neznámou na straně druhé.

S čísly už je to na vás.Možná se to může zdát na poprvé složité, projděte si to tedy ještě jednou, v klidu, krok za krokem. Klidně ještě jednou, dvakrát, pětkrát a nakonec zjistíte, že to vůbec není těžké.
HLAVNĚ SE TENTO POSTUP NEUČTE NAZPAMĚT O TOM MATIKA ANI CHEMIE NEJSOU.

Odpověď 11: Maximální hodnota hmotnostního zlomku je 1, tedy 100 %, a potom se bude jednat o chemicky čistou látku. Dále je rozumné si uvědomit, že součet všech hmotnostních zlomků také musí být 1. Proto, když budu mít roztok o dvou složkách A a B a budu vědět, že w(A) = 0,3, tak poté mohu automaticky dopočítat, že w(B) = 0,7.

Zkusíme společně další typy příkladů. Ty ostatní už budou na vás.

Příklad: Ve 130 g vody bylo rozpuštěno 42 g hydroxidu sodného NaOH. Jaký byl hmotnostní zlomek NaOH v roztoku? Kolika procentní roztok vznikl?

m(NaOH) = 42 g

m(H₂O) = 130 g

w(NaOH) = ?

Tady nám bude stačit prosté dosazení do vzorečku.

Hmotnostní zlomek NaOH v roztoku činil 0,244. Jednalo se tedy o 24,4% roztok.

S nástupem moderních kalkulaček není problém uvádět čísla na spoustu desetinných míst či vůbec nezaokrouhlovat.

Inu, přijde vám výsledek našeho příkladu w(NaOH) = 0,24418604651162790697674418604651 praktický? Dohodneme se, že budeme výsledky uvádět s takovou přesností, jako je uvedené v zadání nebo o jedno desetinné místo více. Je nutné poznamenat, že později, a to zejména při fyzikálních či přesných chemických výpočtech, možná narazíte na tzv. platné číslice a seznam jasných pravidel, jak zaokrouhlovat, ale tím se nyní nebudeme trápit.

Příklad: Jakou hmotnost hydroxidu draselného KOH potřebujeme na přípravu 300 g 5% roztoku?

m(KOH) = ?

m_roztok= 300 g

w(KOH) = 0,05 ≈ 5 %

Známe w(KOH) a m_roztok, proto si m(KOH) ze vzorce snadno vyjádříme.

Na přípravu 300 g 5% roztoku potřebujeme 15 g KOH.

Složitější příklad: Kolik gramů cukru je potřeba rozpustit v 500 ml vody, aby vnikl 15% roztok?

m(cukr) = ?

V(voda) = 500 ml → m(voda) = 500 g

w(cukr) = 0,15≈15%

Známe w(cukr) a m(voda) a spočítat máme m(cukr). Na první pohled budeme čelit problému, protože naši neznámou máme jak v čitateli, tak ve jmenovateli. Kdo si s tím umí poradit, počítejme dál a rovnou dosaďme čísla. Kdo ne, koukněte se na matematické okénko na předešlých stránkách.

Zbavím se zlomků.

Roznásobím závorku.

Převádím m_cukrna levou stranu.

Pro přípravu 15% roztoku je třeba rozpustit 88,23 g cukru v 500 ml vody.

Jde to ale i jednodušeji. Stačí si uvědomit, že součet všech hmotnostních zlomků musí být jedna. Pokud vím, že w(cukr) = 0,15, pak w(voda) musí být 0,85. Tedy 85 % hmotnosti roztoku je tvořeno vodou. Ale my její hmotnost známe. 85 % je tedy 500 g, pak není nic snazšího než spočítat hmotnost celého roztoku. Bude to 588, 23 g. Rozdíl těchto dvou hmotností musí být tedy sůl, 588,23 - 500 = 88,23g.

Další příklady:

Následující příklady jsou těžší. Zkuste je, zapřemýšlejte. Poraďte se s kamarády, a když to nepůjde, zeptejte se na hodině.