Chemie na GJN

Jak jste si jistě všimli, křížové schéma je poměrně snadné a rychle se s ním počítá. Má však jednu velkou nevýhodu. Nelze s ním vyřešit všechny typy příkladů. Když se na chvilku zamyslíte, tak snad odvodíte, s jakým typem přikladu byste narazili. Pokud byste totiž nevěděli hodnotu na středu kříže, velmi špatně by se vám počítalo. Z tohoto důvodu se nyní zaměříme na obecnější postup, který je sice více matematičtější, ale dají se s ním vyřešit všechny typy příkladů.

Směšovací rovnice mají následující tvar:

Kde w_1,2,3 jsou hmotnostní zlomky jednotlivých roztoků a m_1,2,3 jsou hmotnosti jednotlivých roztoků.

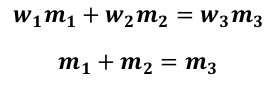
Nejprve se zaměříme na první rovnici. Jaký význam má součin w₁ m₁? Pokud vynásobíme hmotnost roztoku hmotnostním zlomkem roztoku, dostaneme přeci hmotnost čisté látky. První rovnice tedy tvrdí, že pokud sečteme hmotnost čisté látky rozpuštěné v prvním roztoku s hmotností čisté látky rozpuštěné v druhém roztoku, získáme hmotnost čisté látky rozpuštěné v roztoku, který vznikl smícháním prvních dvou. Tomu se ani nedá nic vytknout. Pokud v jednom 250ml hrnku rozpustíte kostku cukru, ve druhém 250ml hrnku rozpustíte tři kostky cukru a oba hrnky slijete dohromady, dostanete roztok, ve kterém jsou rozpuštěny celkem čtyři kostky cukru. Druhá rovnice je mnohem snazší na pochopení. Říká, že výsledný roztok bude mít hmotnost rovnou součtu hmotností původních roztoků.

Příklad:

Jaký hmotnostní zlomek bude mít roztok, který vznikl smícháním 30 g 50% roztoku kyseliny fosforečné a 10 g vody? Všimněte si, že tento příklad by nebyl řešitelný křížovým schématem, protože neznáme prostředek kříže.

1. Krok – zápis

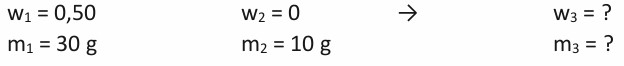
2. Krok – sestavení rovnic

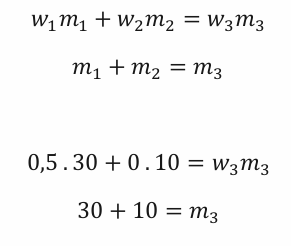
3. Krok – vlastní výpočet
Protože voda je 0% roztokem kyseliny fosforečné, jeden člen první rovnice nám rovnou vypadne. Z druhé rovnice rovnou vidíme m₃. Z druhé rovnice dosadíme za m₃ do první.

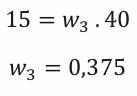
Vzniklý roztok bude mít hmotnostní zlomek roven 0,375.

Příklady k procvičení:

1. Jaký bude hmotnostní zlomek chloridu sodného v roztoku, pokud k 200 g 10% roztoku této soli přidáme 5 g krystalického chloridu sodného? (w(NaCl) = 0,122)
2. Určete hmotnostní zlomek chloridu draselného v roztoku, který vznikl rozpuštěním 2 g chloridu draselného v 0,5 litru jeho 8% roztoku. Hustota 8% roztoku je ρ = 1,05 g . cm ^-3 . (w(KCl) = 0,083)
3. Jaký bude hmotnostní zlomek jodidu draselného, pokud k 200 g jeho roztoku o hmotnostním zlomku 15% přilijeme 50 g 30% roztoku této soli? (w(KI) = 0,18)
4. Jaký bude hmotnostní zlomek fosforečnanu sodného, pokud k 300 g jeho roztoku o hmotnostním zlomku 5% přilijeme 300 g 10% roztoku této soli? (w(Na ₃ PO ₄ ) = 0,075)
5. Jaký bude hmotnostní zlomek síranu sodného v roztoku, který vznikl odpařením 150 g vody z 450 g původně 13% roztoku této soli? (w(Na ₂ SO ₄ ) = 0,195)
6. Jaký bude hmotnostní zlomek roztoku kyseliny sírové, který vznikl slitím200 g 15% roztoku H ₂ SO ₄ 400 cm ³ 30% roztoku H ₂ SO ₄ o hustotě ρ = 1,2185 g . cm ^-3 150 g 10% roztoku H ₂ SO ₄ (w(H ₂ SO ₄ ) = 0,228)
7. Jaký bude hmotnostní zlomek kyseliny chlorovodíkové, který vznikl slitím 200 ml roztoku této kyseliny o molární koncentraci c = 2 mol . dm ^-3 (ρ = 1,05 g . cm ^-3 ) a 50 g 10% roztoku této kyseliny. (w(HCl) = 0,075)
8. Určete hmotnostní zlomek roztoku soli, který vznikl smísením 200 ml roztoku této soli o molární koncentraci c = 4 mol . dm ^-3 a hustotě ρ = 1,23 g . cm ^-3 , 65 g 10% roztoku této soli a 8 g krystalů této soli. Molární hmotnost této soli je M = 142 g . mol ^-1. (w = 0,40)